Een kwadratische vergelijking tekenen: 10 stappen (met afbeeldingen)

2024 Auteur: Robert Blare | [email protected]. Laatst gewijzigd: 2024-02-02 02:08

Wanneer geplot, kwadratische vergelijkingen van de vorm bijl² + bx + c of een(x-h)² + k een gladde U-vormige of een omgekeerde U-vormige curve geven, een parabool genaamd. Het tekenen van een kwadratische vergelijking is een kwestie van het vinden van het hoekpunt, de richting en, vaak, de x- en y-onderscheppingen. In het geval van relatief eenvoudige kwadratische vergelijkingen kan het ook voldoende zijn om een reeks x-waarden in te vullen en een curve te plotten op basis van de resulterende punten. Zie stap 1 hieronder om aan de slag te gaan.

Stappen

Stap 1. Bepaal welke vorm van kwadratische vergelijking je hebt

De kwadratische vergelijking kan in drie verschillende vormen worden geschreven: de standaardvorm, de hoekpuntvorm en de kwadratische vorm. U kunt beide vormen gebruiken om een kwadratische vergelijking te tekenen; het proces voor het tekenen van elk is iets anders. Als je een huiswerkprobleem maakt, krijg je het probleem meestal in een van deze twee vormen - met andere woorden, je zult niet kunnen kiezen, dus het is het beste om beide te begrijpen. De twee vormen van kwadratische vergelijking zijn:

• Standaard vorm.

  In deze vorm wordt de kwadratische vergelijking geschreven als: f(x) = ax² + bx + c waarbij a, b en c reële getallen zijn en a niet gelijk is aan nul.

  Twee standaard kwadratische vergelijkingen zijn bijvoorbeeld f(x) = x² + 2x + 1 en f(x) = 9x² + 10x -8.

• Vertex vorm.

  In deze vorm wordt de kwadratische vergelijking geschreven als: f(x) = a(x - h)² + k waarbij a, h en k reële getallen zijn en a niet gelijk is aan nul. Vertex-vorm wordt zo genoemd omdat h en k je direct het hoekpunt (centraal punt) van je parabool op het punt (h, k) geven.

  Twee vertex-vormvergelijkingen zijn f(x) = 9(x - 4)² + 18 en -3(x - 5)² + 1

• Om een van deze soorten vergelijkingen in een grafiek uit te tekenen, moeten we eerst het hoekpunt van de parabool vinden, het centrale punt (h, k) aan de "tip" van de curve. De coördinaten van het hoekpunt in standaardvorm worden gegeven door: h = -b/2a en k = f(h), terwijl in hoekpuntvorm h en k worden gespecificeerd in de vergelijking.

Stap 2. Definieer uw variabelen

Om een kwadratisch probleem op te lossen, moeten meestal de variabelen a, b en c (of a, h en k) worden gedefinieerd. Een gemiddeld algebraprobleem geeft je een kwadratische vergelijking met de variabelen ingevuld, meestal in standaardvorm, maar soms in hoekpuntvorm.

• Bijvoorbeeld voor de standaardvormvergelijking f(x) = 2x² +16x + 39, we hebben a = 2, b = 16 en c = 39.
• Voor de topvorm vergelijking f(x) = 4(x - 5)² + 12, we hebben a = 4, h = 5 en k = 12.

Stap 3. Bereken h

In vergelijkingen in hoekpuntvorm is uw waarde voor h al gegeven, maar in vergelijkingen in standaardvorm moet deze worden berekend. Onthoud dat voor vergelijkingen in standaardvorm h = -b/2a.

• In ons standaardformuliervoorbeeld (f(x) = 2x² +16x + 39), h = -b/2a = -16/2(2). Oplossend vinden we dat h = - 4.
• In ons voorbeeld van de vertexvorm (f(x) = 4(x - 5)² + 12), weten we h = 5 zonder te rekenen.

Stap 4. Bereken k

Net als bij h is k al bekend in vertex-vormvergelijkingen. Onthoud voor vergelijkingen in standaardvorm dat k = f(h). Met andere woorden, je kunt k vinden door elke instantie van x in je vergelijking te vervangen door de waarde die je zojuist voor h hebt gevonden.

• We hebben in ons standaardformuliervoorbeeld bepaald dat h = -4. Om k te vinden, lossen we onze vergelijking op met onze waarde voor h die x vervangt:

  • k = 2(-4)² + 16(-4) + 39.
  • k = 2(16) - 64 + 39.

  • k = 32 - 64 + 39 =

    Stap 7.

• In ons voorbeeld van de vertexvorm kennen we opnieuw de waarde van k (wat 12 is) zonder dat we iets hoeven te rekenen.

Stap 5. Plot uw hoekpunt

Het hoekpunt van je parabool is het punt (h, k) - h specificeert de x-coördinaat, terwijl k de y-coördinaat specificeert. Het hoekpunt is het centrale punt in je parabool - ofwel de onderkant van een 'U' of de top van een omgekeerde 'U'. Het kennen van het hoekpunt is een essentieel onderdeel van het tekenen van een nauwkeurige parabool - vaak, in schoolwerk, is het specificeren van het hoekpunt een verplicht onderdeel van een vraag.

• In ons voorbeeld van een standaardformulier bevindt ons hoekpunt zich op (-4, 7). Onze parabool zal dus 4 spaties links van 0 en 7 spaties boven (0, 0) pieken. We moeten dit punt in onze grafiek plotten, waarbij we de coördinaten moeten labelen.
• In ons voorbeeld van de vertex-vorm bevindt onze vertex zich op (5, 12). We moeten een punt 5 spaties naar rechts plotten en 12 spaties erboven (0, 0).

Stap 6. Teken de as van de parabool (optioneel)

De symmetrieas van een parabool is de lijn die door het midden loopt en deze perfect in tweeën deelt. Over deze as zal de linkerkant van de parabool de rechterkant spiegelen. Voor kwadraten van de vorm ax² + bx + c of a(x - h)² + k, de as is een lijn evenwijdig aan de y-as (met andere woorden, perfect verticaal) en door het hoekpunt.

In het geval van ons standaardformuliervoorbeeld is de as een lijn evenwijdig aan de y-as en door het punt (-4, 7). Hoewel het geen deel uitmaakt van de parabool zelf, kan het lichtjes markeren van deze lijn in je grafiek je uiteindelijk helpen om te zien hoe de parabool symmetrisch kromt

Stap 7. Zoek de openingsrichting

Nadat we het hoekpunt en de as van de parabool hebben uitgezocht, moeten we vervolgens weten of de parabool naar boven of naar beneden opent. Gelukkig is dit eenvoudig. Als "a" positief is, zal de parabool naar boven openen, terwijl als "a" negatief is, de parabool naar beneden zal openen (d.w.z. hij zal ondersteboven worden gedraaid).

• Voor ons standaardformuliervoorbeeld (f(x) = 2x² +16x + 39), weten we dat we een parabool hebben die naar boven opent omdat, in onze vergelijking, a = 2 (positief).
• Voor ons voorbeeld van de vertexvorm (f(x) = 4(x - 5)² + 12), weten we dat we ook een parabool hebben die naar boven opent omdat a = 4 (positief).

Stap 8. Zoek en plot zo nodig x intercepts

Vaak wordt u bij schoolwerk gevraagd om de x-snijpunten van een parabool te vinden (dit zijn een of twee punten waar de parabool de x-as raakt). Zelfs als je ze niet kunt vinden, kunnen deze twee punten van onschatbare waarde zijn voor het tekenen van een nauwkeurige parabool. Niet alle parabolen hebben echter x-intercepts. Als uw parabool een hoekpunt heeft dat naar boven opent en een hoekpunt boven de x-as heeft of als het naar beneden opent en een hoekpunt onder de x-as heeft, het zal geen x onderschept hebben. Los anders uw x-onderscheppingen op met een van de volgende methoden:

• Stel gewoon f(x) = 0 in en los de vergelijking op. Deze methode kan werken voor eenvoudige kwadratische vergelijkingen, vooral in de vorm van een hoekpunt, maar zal buitengewoon moeilijk blijken te zijn voor meer gecompliceerde. Zie hieronder voor een voorbeeld

  • f(x) = 4(x - 12)² - 4
  • 0 = 4(x - 12)² - 4
  • 4 = 4(x - 12)²
  • 1 = (x - 12)²
  • SqRt(1) = (x - 12)
  • +/- 1 = x -12. x = 11 en 13 zijn de x-snijpunten van de parabool.

• Factor uw vergelijking. Enkele vergelijkingen in de ax² + bx + c-vorm kan gemakkelijk worden verwerkt in de vorm (dx + e)(fx +g), waarbij dx × fx = ax², (dx × g + fx × e) = bx, en e × g = c. In dit geval zijn uw x-onderscheppingen de waarden voor x die beide termen tussen haakjes = 0 maken. Bijvoorbeeld:

  • x² + 2x + 1
  • = (x + 1)(x + 1)
  • In dit geval is uw enige x-snijpunt -1 omdat het instellen van x gelijk aan -1 ervoor zorgt dat een van de ontbonden termen tussen haakjes gelijk is aan 0.

• Gebruik de kwadratische formule. Als u uw x-onderscheppingen niet gemakkelijk kunt oplossen of uw vergelijking kunt ontbinden, gebruik dan een speciale vergelijking, de kwadratische formule die voor dit doel is ontworpen. Als dit nog niet het geval is, zet u uw vergelijking in de vorm ax² + bx + c, sluit dan a, b en c aan in de formule x = (-b +/- SqRt(b² - 4ac))/2a. Merk op dat dit je vaak twee antwoorden geeft voor x, wat OK is - dit betekent alleen dat je parabool twee x-onderscheppingen heeft. Zie hieronder voor een voorbeeld:

  • -5x² + 1x + 10 wordt als volgt in de kwadratische formule ingeplugd:
  • x = (-1 +/- SqRt(1² - 4(-5)(10)))/2(-5)
  • x = (-1 +/- SqRt(1 + 200))/-10
  • x = (-1 +/- SqRt(201))/-10
  • x = (-1 +/- 14,18)/-10
  • x = (13,18/-10) en (-15,18/-10). De x-onderscheppingen van de parabool zijn ongeveer x = - 1.318 en 1.518
  • Ons vorige standaardformuliervoorbeeld, 2x² + 16x + 39 wordt als volgt in de kwadratische formule ingeplugd:
  • x = (-16 +/- SqRt (16² - 4(2)(39)))/2(2)
  • x = (-16 +/- SqRt (256 - 312))/4
  • x = (-16 +/- SqRt(-56)/-10
  • Omdat het onmogelijk is om de vierkantswortel van een negatief getal te vinden, weten we dat: geen x onderschept bestaan voor deze specifieke parabool.

Stap 9. Zoek en plot zo nodig het y-snijpunt

Hoewel het vaak niet nodig is om het y-snijpunt van een vergelijking te vinden (het punt waarop de parabool door de y-as gaat), kan dit uiteindelijk nodig zijn, vooral als je op school zit. Dit proces is vrij eenvoudig - stel gewoon x = 0 in en los vervolgens uw vergelijking op voor f (x) of y, wat u de y-waarde geeft waarbij uw parabool door de y-as gaat. In tegenstelling tot x-onderscheppingen, kunnen standaardparabolen slechts één y-snijpunt hebben. Opmerking - voor vergelijkingen in standaardvorm is het snijpunt y bij y = c.

• We kennen bijvoorbeeld onze kwadratische vergelijking 2x² + 16x + 39 heeft een y-snijpunt bij y = 39, maar het kan ook als volgt worden gevonden:

  • f(x) = 2x² + 16x + 39
  • f(x) = 2(0)² + 16(0) + 39

  • f(x) = 39. Het y-snijpunt van de parabool is at j = 39.

    Zoals hierboven opgemerkt, is het y-snijpunt bij y = c.

• Onze vertex vorm vergelijking 4(x - 5)² + 12 heeft een y-snijpunt dat als volgt kan worden gevonden:

  • f(x) = 4(x - 5)² + 12
  • f(x) = 4(0 - 5)² + 12
  • f(x) = 4(-5)² + 12
  • f(x) = 4(25) + 12

  • f(x) = 112. Het y-snijpunt van de parabool is at j = 112.

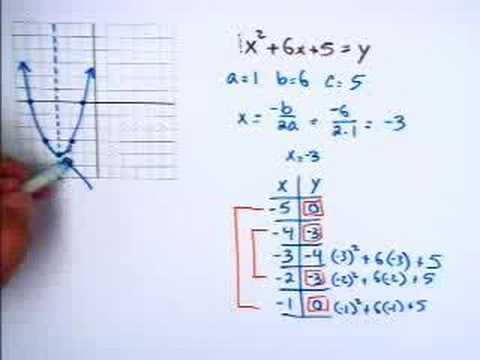
Stap 10. Teken indien nodig extra punten en maak vervolgens een grafiek

U zou nu een hoekpunt, richting, x-snijpunt(en) en mogelijk een y-snijpunt voor uw vergelijking moeten hebben. Op dit punt kunt u proberen uw parabool te tekenen met behulp van de punten die u als richtlijn hebt, of u kunt meer punten vinden om uw parabool te "vullen", zodat de curve die u tekent nauwkeuriger is. De eenvoudigste manier om dit te doen, is door een paar x-waarden aan weerszijden van uw hoekpunt in te voeren en deze punten vervolgens te plotten met behulp van de y-waarden die u verkrijgt. Vaak vereisen leraren dat je een bepaald aantal punten behaalt voordat je je parabool tekent.

• Laten we de vergelijking x. opnieuw bekijken² + 2x + 1. We weten al dat het enige x-snijpunt op x = -1 ligt. Omdat het het x-snijpunt slechts op één punt raakt, kunnen we afleiden dat het hoekpunt het x-snijpunt is, wat betekent dat het hoekpunt (-1, 0) is. We hebben in feite maar één punt voor deze parabool - lang niet genoeg om een goede parabool te tekenen. Laten we er nog een paar zoeken om ervoor te zorgen dat we een nauwkeurige grafiek tekenen.

  • Laten we de y-waarden zoeken voor de volgende x-waarden: 0, 1, -2 en -3.
  • Voor 0: f(x) = (0)² + 2(0) + 1 = 1. Ons punt is (0, 1).

  • Voor 1: f(x) = (1)² + 2(1) + 1 = 4. Ons punt is: (1, 4).

  • Voor -2: f(x) = (-2)² + 2(-2) + 1 = 1. Ons punt is (-2, 1).

  • Voor -3: f(x) = (-3)² + 2(-3) + 1 = 4. Ons punt is (-3, 4).

  • Zet deze punten in de grafiek en teken uw U-vormige curve. Merk op dat de parabool perfect symmetrisch is - wanneer je punten aan de ene kant van de parabool op hele getallen liggen, kun je jezelf meestal wat werk besparen door simpelweg een bepaald punt over de symmetrieas van de parabool te reflecteren om het corresponderende punt aan de andere kant te vinden van de parabool.

Video - Door deze service te gebruiken, kan bepaalde informatie worden gedeeld met YouTube

Tips

• Merk op dat in f(x) = ax² + bx + c, als b of c gelijk is aan nul, verdwijnen die getallen. Bijvoorbeeld 12x² + 0x + 6 wordt 12x² + 6 omdat 0x 0 is.
• Rond getallen af of gebruik breuken zoals je algebraleraar je zegt. Dit zal u helpen om uw kwadratische vergelijkingen correct te plotten.